专业术语
- 标签(y)–我们要预测的真实事物
- 特征(x)–描述数据的输入变量
- 样本–数据的特征实例。分为“有标签样本”和“无标签样本”
- 模型–特征与标签之间的关系。分为“回归模型”和“分类模型”
- 损失–衡量模型优劣的一个数值。平方损失(L2损失),均方误差(MSE)
线性回归
- y = b + w1x1
y表示标签
b(bias)偏差
w1(weight)权重1
x1特征1
降低损失(Reducing Loss)
如何降低损失?
- 梯度下降法。降低损失本质上就是计算损失函数的最小值,也是计算最佳权重和偏差值,样本选取上不能采用单个样本,也不能选取所有样本,而是采用“小批量梯度下降法”,选取10-1000个样本。学习时,输入样本,得到一个损失函数关于w的函数,给权重设置一个初始值,求权重在该点的倒数即可得到在改点损失函数是下降还是上升的,然后以一定步进值在下降的方向变换权重值。
- 迭代方法。给权重和偏差设置一个初值,然后不断的迭代直到损失尽可能低。
- 学习速率。梯度下降法中,变化权重值时,将当前梯度乘以一个标量(步进),这个标量为学习速率,比如当前梯度为2,学习速率为0.25,则下一个权重点为1.5。
常用工具包Pandas
- 导入 import pandas as pd
- 创建Series对象,population = pd.Series([100,200,300])
- 创建DataFrame对象,dataframe = pd.DataFrame(‘popu’:population)
- 显示dataframe前几条数据,dataframe.head()
- 访问数据,dataframe[‘popu’]返回一个列表,datafreame[‘popu’][1]返回某一列表的某个值
- 对单列Series进行转换,population.apply(lambda x : x > 150)返回一个新的boolean型Series
- 将DataFrame重新排序,dataframe.reindex[0,1],dataframe.reindex(np.random.permutation(dataframe.index))将dataframe随机排序
构建第一个模型
定义特征值并配置特征列。在TensorFlow中,我们使用一种称为“特征列”的结构来表示特征的数据类型,“特征列”仅存储对特征数据的描述,不包含特征数据本身。特征列将原始数据与模型需要的数据联系起来
定义一个数字型特征列:1
tf.feature_column.numeric_column("total_rooms")
定义目标(标签)
1
targes = dataframe["median_house_value"]
配置LinearRegressor
1
2
3
4
5#使用梯度下降优化器训练模型
my_optimizer = tf.train.GradientDescentOptimizer(lerning_rate = 0.000001)
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer,5.0)
#使用特征列和优化器配置一个线性回归模型
linear_regressor = tf.estimator.Linearregressor(feature_column=feature_column,optimizer=my_optimizer)定义输入函数,让特征与标签有个入口
- 调用模型的train()方法训练模型
- 将特征输入到模型,得到预算值,计算损失
- 识别离群值,截取离群值,重新训练
泛化
- 如果一个模型尝试紧密拟合训练数据,但是不能很好的泛化新的数据,就会发生过拟合
训练集和测试集
- 将单个数据集拆分成一个训练集和测试集
- 保证测试集满足如下两个条件:
- 规模足够大,可产生具有统计意义的结果
- 能代表整个数据集
- 训练过程中,不断调整超参数对训练集进行训练,来达成测试集的损失最小,这样有一个问题,那就是容易造成过拟合。解决方法:从训练集内部再划分一个验证集出来,在验证集的基础上不断调整参数,最后再在测试集上进行测试
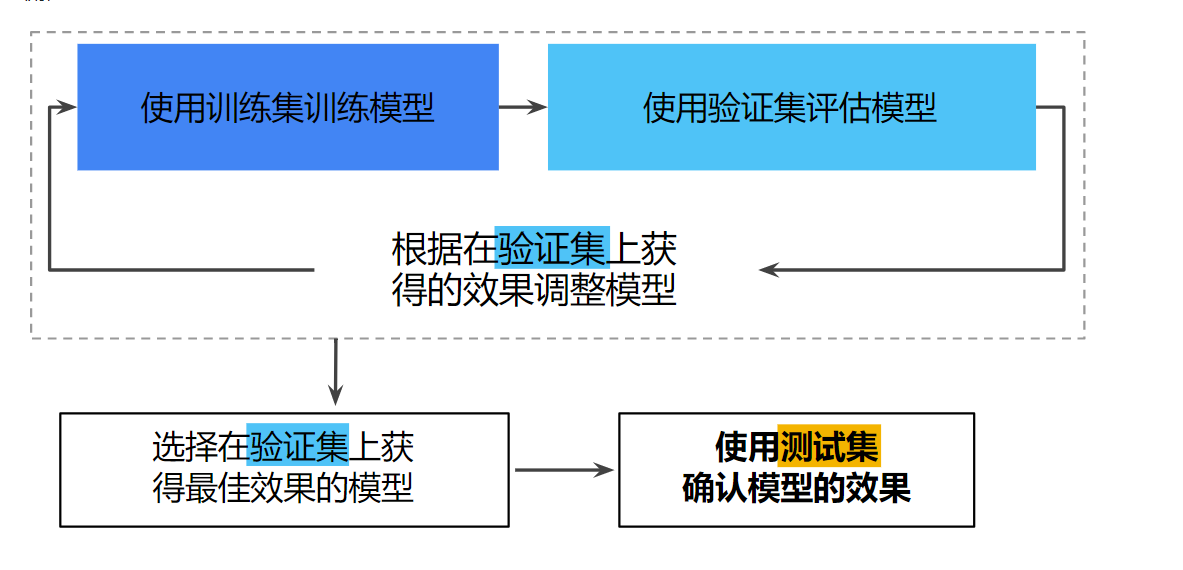
- 机器学习中的调试通常是数据调试而不是代码调试
特征工程
- 从原始数据创建特征的过程称为特征工程
- 良好特征具备的特性:
- 以非零值的形式在数据集中多次出现
- 具备明确的含义,唯一性的值不适合做特征,如house_age:845465就不适合
- 特征不应该使用“魔术”值,超出范围的值
- 特征值不应该随时间而变化
- 不应包含离谱的离群值
- 分箱技巧
- 特征有时候需要组合,在预测一个地区的房价时,单独把经度当作特征明显不恰当,如果把经度和纬度分别分箱,然后在交叉组合,这样得到的特征组合就表示地图上的特定区域了
数据分析
- dataframe.corr()函数将返回完整的相关系数或协方差矩阵
-1.0:完全负相关
0.0:不相关
1.0:完全正相关 - 选取相关性强的特征作为输入
- 特征组合,特征组合是指将两个或多个输入特征相乘生成新的特征
正则化(Regularization)
某个模型在训练过程中训练损失逐渐减小,但是验证损失最终增加,这时候就产生了过拟合。为了防止过拟合,我们可以降低复杂模型的复杂度(可以理解为wx的项数)来防止过拟合,这种过程称为正则化。也就是说并非以最小损失为目标,而是以最小损失和复杂度为目标。L2正则会使所有权重趋于0.0。
- L2正则化可以使权重趋于0.0,但是并不能使权重为0.0,在处罚高权重的时候是除以一个数
- L1正则化可以使权重为0,在处罚高权重的时候是减去一个数,L1正则适用于将高维度的组合特征项权重降为0
1
tf.train.FtrlOptimizer(learning_rate=learning_rate,ll_regularization_strength=regularization_strength)
逻辑回归
- 逻辑回归模型要求feature_targets为1.0或0.0,同时将feature_column修改成bucketized_column(),再将创建模型函数修改成tf.estimator.LinearClassifier()即可
- 对数损失函数是逻辑回归的损失函数
LogLoss = ∑(-ylog(y’) - (1-y)log(1-y’)) - 阈值–逻辑判断中的临界值
- 准确率–预测结果与实际值一致 / 总样本数
- 精确率–预测结果为正的正确个数 / 预测结果为正的总个数(小男孩说狼来了中有多少次是对的)
- 召回率–正样本中被预测正确的个数 / 正样本总个数(在所有试图进入村中的狼中,我们发现了多少头)
- 真正例率(TPR)–真实的正例中,被预测为正例的比例,同召回率
假正例率(FPR)–真实的反例中,被预测为正例的比例
精确率和召回率是此消彼长的状态,提高阈值可能会提高精确率,同时可能会降低召回率
- 预测偏差–预测的偏差应约等于“观察平均值”
神经网络(Neural Networks)
- 激活函数–输入与输出之间添加一层非线性的函数
- 非线性激活函数可以学习非线性模型,如果一个模型具有2个隐藏层,那么学习模型需要一定的时间,而且学习结果有很大的不确定性,有时损失很低,有时差异很大
- 添加隐藏层和额外节点可以让模型结果看起来大致相同,每次运行结果差异较小
1
2
3
4
5
6#使用DNNRegressor类定义神经网络结构,hidden_units=[3,10]定义了两个隐藏层,第一层包括3个节点,第二层包括10个节点
my_optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer,5.0)
DNNRegressor = tf.estimator.DNNRegressor(
feature_column=construct_feature_columns(training_examples),
hidden_units=[3,10])
神经网络的优化
- 使用线性缩放将特征标准化。

也可使用其他标准化函数,将特征以柱状图的形式显示,对数形式的特征适合使用log函数,均匀分布的使用线性缩放函数,部分有极端离群值的特征采用截取函数
尝试使用其他的优化器。
AdaGrad的核心是灵活的修改模型中每个系数的学习率,从而单调降低有效的学习率,该优化器对凸优化问题非常有效,这个优化器需要指定较大的学习率
1
my_optimizer=tf.train.AdagradOptimizer(learning_rate=0.0007)
对于非凸优化问题,Adam有时比AdaGrad更有效
1
my_optimizer=tf.train.AdamOptimizer(learning_rate=0.0007)
多类别神经网络(Multi-Class Neural Networks)
- 当要识别多个标签时,不能单独为每个标签创建一个二分类器。
- 在多类别识别问题中,Softmax为每个类别分配一个小数作为概率,所有类别的概率加起来和为1,这样更有利于收敛
- Softmax层是紧挨着输出层之前的神经网络层,Softmax层必须和输出层拥有一样的节点数
- Softmax的识别结果只有一个,如果要同时识别多个,得改用多个逻辑回归